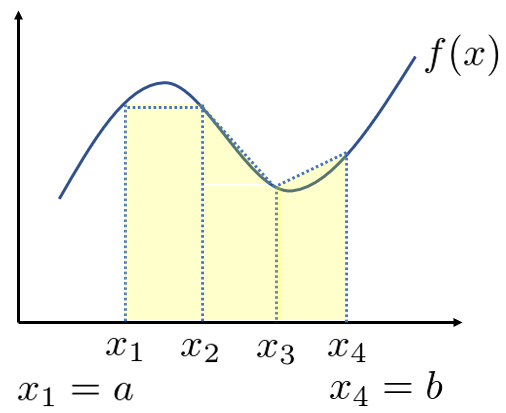
台形公式
補間多項式の記事で求めた補間多項式を用いて、積分近似してみます。
で
は以下のようにおきました。
は
によらない定数ですが、計算が大変なため、求めません。
の近似のための
の計算式をニュートン・コーツの公式といいます。
ニュートン・コーツの公式での場合を台形公式といいます。
関数に対する台形公式は、次のように書けます。
を示します。
[証明]
のとき、
で、以下が成り立ちます。
を求めます。
を求めます。
とニュートン・コーツの公式より
となります。
[証明終わり]
台形公式のイメージは以下の図です。
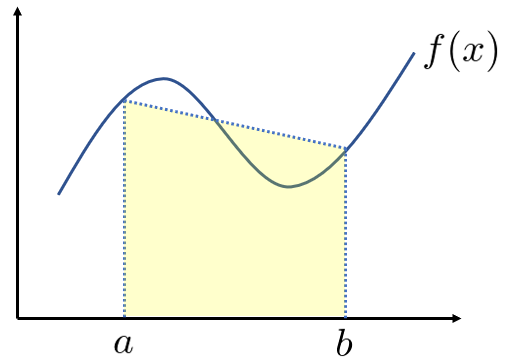
複合台形公式の実験
のグラフは下図のようになります。
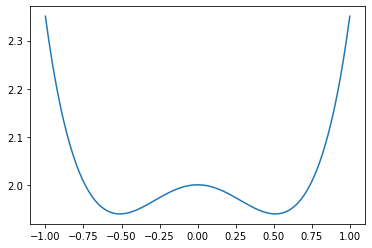
先に解析解を計算してみます。
次にプログラムを使って、近似解を
を変更して求めてみました。
青の点線が解析解でオレンジ色が近似解です。横軸がで、縦軸が解析解及び近似解の値です。
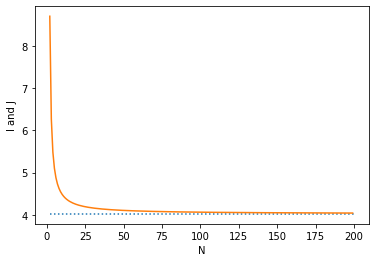
が大きくなると、
と
は近い値を取ることが分かります。
偉人の名言

あせってはいけません。
ただ、牛のように、図々しく進んで行くのが大事です。
夏目漱石
参考文献
モンテカルロ統計計算
動画
なし