凸計画問題と最適化 - 機械学習基礎理論独習

凸集合

空でない集合 $S(\subset{\mathbb R}^n)$ 内の任意の2つのベクトル ${\bf x}_1,{\bf x}_2\in S$ と、
$0\leq\lambda\leq 1$ を満たす任意の実数 $\lambda$ に対して、

$\begin{eqnarray} \lambda{\bf x}_1+(1-\lambda){\bf x}_2\in S\tag{1} \end{eqnarray}$

が成り立つとき、 $S$ を凸集合といいます。
凸集合と非凸集合のイメージを下に記します。
f:id:olj611:20210918195159p:plain:w600

凸関数

凸集合 $S(\subset{\mathbb R}^n)$ 上で定義された関数 $f:S\rightarrow{\mathbb R}^1$ が、
$S$ 内の任意の2つのベクトル ${\bf x}_1,{\bf x}_2$ と、 $0\leq\lambda\leq 1$ なる任意の $\lambda$ に対して

$\begin{eqnarray} f(\lambda{\bf x}_1+(1-\lambda){\bf x}_2)\leq\lambda f({\bf x}_1)+(1-\lambda)f({\bf x}_2)\tag{2} \end{eqnarray}$

を満たすとき、 $f({\bf x})$ は $S$ 上で凸関数であるといいます。

また、 $S$ 内の ${\bf x}_1\not={\bf x}_2$ なる任意の2つのベクトル ${\bf x}_1,{\bf x}_2$ と、 $0\leq\lambda\leq 1$ なる任意の $\lambda$ に対して

$\begin{eqnarray} f(\lambda{\bf x}_1+(1-\lambda){\bf x}_2) < \lambda f({\bf x}_1)+(1-\lambda)f({\bf x}_2)\tag{3} \end{eqnarray}$

を満たすとき、 $f({\bf x})$ は $S$ 上で狭義凸関数であるといいます。
狭義凸関数と凸関数と非凸関数のイメージを下に記します。
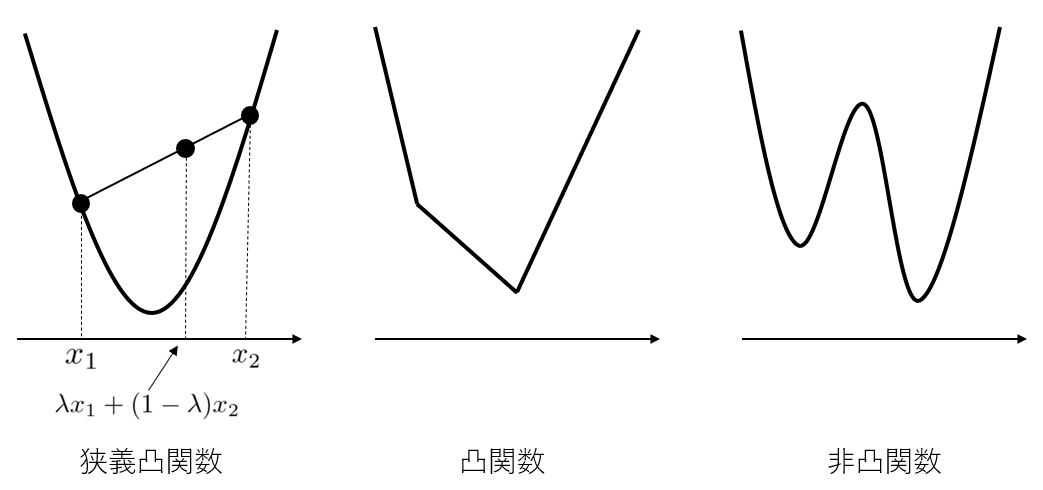
f:id:olj611:20210918200544p:plain:w600

なお、凹関数という言葉もありますが、凸関数と凹関数は上下が逆になっているだけで、いずれも凸性を有しており、
両者に本質的な違いはありません。
凹関数という言葉は個人的にあまり使われないように思います。

凸関数とヘッセ行列の関係について、次の定理が成り立ちます。

定理1(証明略)
凸集合 $S(\subset{\mathbb R}^n)$ 上で2回連続微分可能な関数 $f:S\rightarrow{\mathbb R}^1$ が
凸関数であるための必要十分条件は、そのヘッセ行列 ${\bf H}$ が $S$ 上で半正定値となることである。

定理2(証明略)
関数 $f({\bf x})$ のヘッセ行列 ${\bf H}$ が $S$ 上で正定値ならば、 $f({\bf x})$ は狭義凸関数である。
ただし、その逆は成り立たない。

最適化問題

最適化問題とは、「ある制約条件の下で特定の関数を最小化、あるいは最大化する問題」のことです。
最小化、あるいは最大化の対象となる関数を目的関数といいます。
目的関数として、 $n$ 次元ベクトル ${\bf x}$ の実関数 $f({\bf x})$ を考えます。
目的関数 $f({\bf x})$ の最大化は $-f({\bf x})$ の最小化と等価であるので、以後最適化問題とは最小化問題のことであるとして進めます。
最適化における制約条件は、一般に次のように書けます。

$\begin{eqnarray} \left\{ \begin{array}{l} {\bf x}\in S\\ S=\{{\bf x}|条件\} \end{array}\tag{4} \right. \end{eqnarray}$

ここで、式 $(4)$ の「条件」は、一般に ${\bf x}$ に関する不等式で示されることが多いです。
式 $(4)$ の $S$ は、制約条件を満たす点の集合を表しており、実行可能領域といいます。
以上をまとめると、最適化問題とは、
「実行可能領域 $S$ において、目的関数 $f({\bf x})$ を最小化する ${\bf x}={\bf x}^*$ を見出す問題」といえます。
式で書くと、

$\begin{eqnarray} \end{eqnarray}$

$\newcommand{\argmin}{\mathop{\rm arg~min}\limits}\begin{eqnarray} {\bf x}^*=\argmin_{{\bf x}} \{f({\bf x})|{\bf x}\in S\}\tag{5} \end{eqnarray}$

となります。この ${\bf x}^*$ を最適解といいます。
式 $(5)$ で示される最適解は、実行可能領域 $S$ 全体で目的関数 $f({\bf x})$ を最小化する解であり、
大域的最適解といいます。
一方、実行可能領域内のある点が、その近傍のどの点よりも目的関数を小さくできる時、
その点を局所的最適解といいます。
下図に1次元の場合の大域的最適解と局所的最適解の例を示します。
f:id:olj611:20210918213504p:plain:w300

式 $(5)$ で示した最適化問題において、実行可能領域が凸集合であり、目的関数が凸関数の場合、
この問題を凸計画問題といいます。
凸計画問題については次の定理が成り立ちます。
定理3(証明略)
最適化問題が凸計画問題であれば、局所的最適解は大域的最適解である。
さらに、目的関数が狭義凸関数のとき、大域的最適解が存在すれば、唯一である。

偉人の名言

f:id:olj611:20210918214036p:plain:w300
面白きこともなき世を面白く住みなすものは心なりけり
高杉晋作

参考文献

続・わかりやすいパターン認識 p291-p297

動画

なし