関数解析③～距離空間における種々の定義～

概要

開球、有界な集合、有界な点列、部分列、収束列、コーシー列の定義

開球、有界な集合、有界な点列、部分列

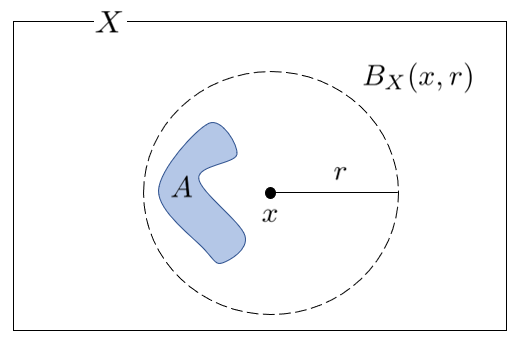
・ $(X,d)$ を距離空間とする。
(i) $x\in X,\ r>0$ とする。
$B_X(x,r):=\{y\in X\ |\ d(x,y) < r\}$ を " $x$ を中心とする半径 $r$ の開球" という。

(ii) $A\subset X$ に対し、 $\exists x\in X$ と $\exists r > 0\ s.t. A\subset B_x(x,r)$ となるとき、 " $A$ は有界" であるという。

(iii) $X$ の点列 $\bigl\{x_n\bigr\}_{n=1}^\infty\subset X$ に対し、
$\{x_n\in X\ |\ n=1,2,\ldots\}\subset X$ が有界であるとき、" $\bigl\{x_n\bigr\}_{n=1}^\infty$ は有界な点列"であるという。

(iv) $\bigl\{x_n\bigr\}_{n=1}^\infty$ を $X$ の点列とする。
このとき、 $\bigl\{n_k\bigr\}_{k=1}^\infty\subset{\mathbb N}$ で、 $n_1 < n_2 < n_3\cdots\ (\displaystyle\lim_{k\rightarrow\infty}n_k=\infty)$ なる数列 $\bigl\{n_k\bigr\}_{k=1}^\infty$ に対し、
$\bigl\{x_{n_k}\bigr\}_{n=1}^\infty$ を " $\bigl\{x_n\bigr\}_{n=1}^\infty$ の部分列" という。

収束列、コーシー列

・ $(X,d)$ を距離空間とする。
(i) 点列 $\bigl\{x_n\bigr\}_{n=1}^\infty\subset X$ と点 $x\in X$ に対し、 $\displaystyle\lim_{n\rightarrow\infty}d(x_n,x)=0$ となるとき、
" $\bigl\{x_n\bigr\}_{n=1}^\infty$ は収束列" であるといい、 $\displaystyle\lim_{n\rightarrow\infty}x_n=x$ または $x_n\rightarrow x\ (n\rightarrow\infty)$ と書く。

(ii) 点列 $\bigl\{x_n\bigr\}_{n=1}^\infty\subset X$ に対し、 $\displaystyle\lim_{n,m\rightarrow\infty}d(x_n,x_m)=0$ となるとき、" $\bigl\{x_n\bigr\}_{n=1}^\infty$ はコーシー列" であるという。

注意
・ $\displaystyle\lim_{n\rightarrow\infty}d(x_n,x)=0$ (収束列) $\Leftrightarrow\forall\epsilon>0,\exists n_0\in{\mathbb N},\forall n\geq n_0, d(x_n,x)<\epsilon$
・ $\displaystyle\lim_{n,m\rightarrow\infty}d(x_n,x_m)=0\Leftrightarrow\forall\epsilon>0,\exists n_0\in{\mathbb N},\forall n,m\geq n_0, d(x_n,x_m)<\epsilon$

機械学習基礎理論独習

誤りがあればご指摘いただけると幸いです。数式が整うまで少し時間かかります。リンクフリーです。

関数解析③～距離空間における種々の定義～

概要

開球、有界な集合、有界な点列、部分列

収束列、コーシー列