正則化の意味

正則化

目的関数に正則化項を加えることにより、過学習を防ぐことができます。
一般的な正則化項を用いて目的関数を表してみます。

$\begin{eqnarray} &&E({\bf w})=\frac{1}{2}\sum_{n=1}^N(t_n-{\bf w}^\top{\boldsymbol\phi}({\bf x}_n))^2+\frac{\lambda}{2}\sum_{j=1}^M|w_j|^q\tag{1}\\ \end{eqnarray}$

(1)において、 $q=1$ の時をラッソ回帰、 $q=2$ の時をリッジ回帰というのでした。
異なる $q$ の値に対する正則化関数のグラフを示します。

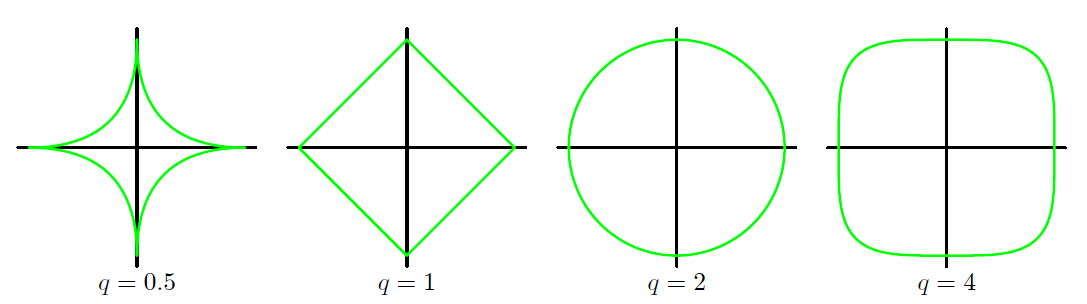
f:id:olj611:20210313011528p:plain:w800

$\begin{eqnarray} &&E_D({\bf w})=\frac{1}{2}\sum_{n=1}^N(t_n-{\bf w}^\top{\boldsymbol\phi}({\bf x}_n))^2\tag{2}\\ &&\sum_{j=1}^M|w_j|^q\leq\eta\tag{3}\\ \end{eqnarray}$

正則化していない目的関数(2)を、(3)の制約条件の下で最小化することを考えます。

(3)を変形します。

$\begin{eqnarray} &&\frac{1}{2}\left(\sum_{j=1}^M|w_j|^q-\eta\right)\leq0\tag{4}\\ \end{eqnarray}$

(2)、(4)より、ラグランジュ関数は以下のようになります。

$\begin{eqnarray} L({\bf w},\lambda)=\frac{1}{2}\sum_{n=1}^N(t_n-{\bf w}^\top{\boldsymbol\phi}({\bf x}_n))^2+\frac{\lambda}{2}\left(\sum_{j=1}^M|w_j|^q-\eta\right)\tag{5} \end{eqnarray}$