ベルンシュタインの定理とは
ベルンシュタインの定理は集合の濃度に関する定理で、とても重要です。
ベルンシュタインの定理は以下のように言い換えもできます。
ベルンシュタインの定理の言いかえ 
証明
単射 と
が存在したとする。任意の
に対して、
の部分集合
を
のイメージを図1に記しておきます。
図1

次に、 を満たす
の部分集合
全体からなる集合族を
とします。
要は、
ここで、
このとき、等式
まず、 を示します。
任意の に対して、
であり、また、
なので、
より
また、
次に、 を示します。
であり、
より、
なので、
より、
が成り立つので、
。(
の定義を確認してください。)
ゆえに、
以上より、 が成り立つことが示せました。
よって、 が成り立つから、
図2

このとき、
その逆写像
図3
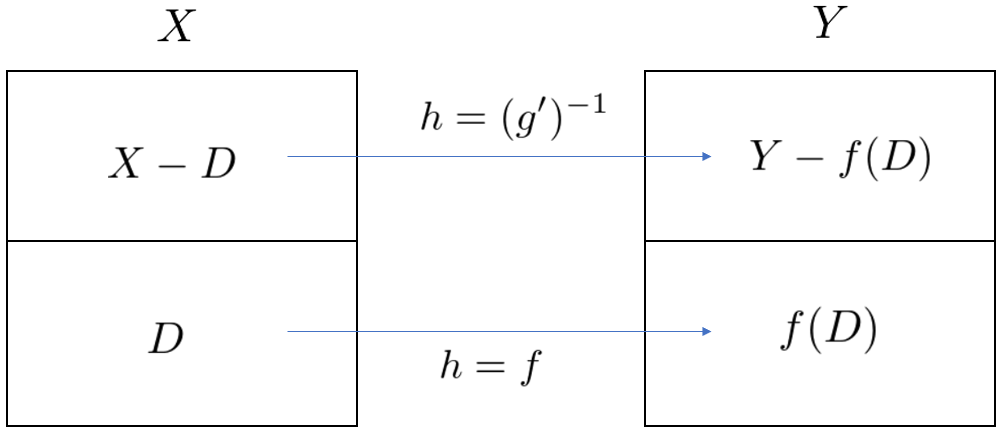
最後に
Web上には、ベルンシュタインの定理の証明は帰納法を使ったものが多かったので、帰納法を使わない証明を記事化しました。
ポイントは、 の箇所かと思います。
帰納法を使った証明も記事化予定です。(ホンマか?)
参考文献
はじめての集合と位相 p75-p76