条件付き独立性

3変数 $a,b,c$ を考えます。
$b$ および $c$ が与えられたとき、 $a$ の条件付き分布が $b$ の値に依存しないとします。
式で書くと以下のようになります。

$\begin{eqnarray} p(a|b,c)=p(a|c)\tag{1} \end{eqnarray}$

このとき、 $c$ が与えられた下で、 $a$ は $b$ に対して、条件付き独立であるといいます。
この条件付き独立は次のようにも表せます。

$\begin{eqnarray} p(a,b|c)&=&p(a|b,c)p(b|c)\\ &=&p(a|c)p(b|c)\tag{2} \end{eqnarray}$

また、次のような記法でも表せます。

$\begin{eqnarray} a\mathop{\perp\!\!\!\!\perp}b|c\tag{3} \end{eqnarray}$

以下で、条件付き独立を考える上で大事な3つのパターンを紹介します。

tail-to-tail

まず、tail-to-tailです。
$c$ が2本のリンクの矢印の尾(英語でtail)で接続しているので、tail-to-tailといいます。
$c$ が未観測の時のグラフは以下のようになります。

図1: $c$ が未観測の時のtail-to-tail
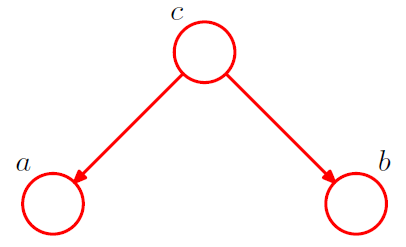
f:id:olj611:20210930021433p:plain:w250

図1の有向グラフより、同時分布を書くと次のようになります。

$\begin{eqnarray} p(a,b,c)=p(a|c)p(b|c)p(c)\tag{4} \end{eqnarray}$

$a,b$ の独立性を調べるため、式 $(4)$ を $c$ で周辺化します。

$\begin{eqnarray} p(a,b)=\sum_cp(a|c)p(b|c)p(c)\tag{5} \end{eqnarray}$

式 $(5)$ は一般には $p(a)p(b)$ の形には書けないので、

$\begin{eqnarray} a\mathop{\not\perp\!\!\!\!\!\!\perp}b|\emptyset\tag{6} \end{eqnarray}$

が言えます。
ここで、 $\emptyset$ は空集合、 $\mathop{\not\perp\!\!\!\!\!\!\perp}$ は条件付き独立性が「一般には」成立しないことを意味します。

$c$ が観測されたとします。この時、グラフは以下のようになります。

図2: $c$ が観測された時のtail-to-tail
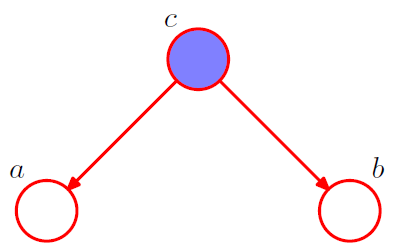
f:id:olj611:20210930021450p:plain:w250

図2の有向グラフより、同時分布を書くと次のようになります。

$\begin{eqnarray} p(a,b|c)&=&\frac{p(a,b,c)}{p(c)}\\ &=&\frac{p(a|c)p(b|c)p(c)}{p(c)}\\ &=&p(a|c)p(b|c)\tag{7} \end{eqnarray}$

式 $(7)$ より、

$\begin{eqnarray} a\mathop{\perp\!\!\!\!\perp}b|c\tag{8} \end{eqnarray}$

が言えます。

これは元々独立ではなかった $a,b$ が、 $c$ が観測されたことにより、独立になったことを意味しています。

head-to-tail

次に、head-to-tailです。
$c$ が1本のリンクは矢印の先(英語でhead)で、もう1本のリンクは矢印の尾(英語でtail)で接続しているので、head-to-tailといいます。
※tail-to-headとはいいません。
$c$ が未観測の時のグラフは以下のようになります。

図3: $c$ が未観測の時のhead-to-tail
f:id:olj611:20210930021504p:plain:w300

図3の有向グラフより、同時分布を書くと次のようになります。

$\begin{eqnarray} p(a,b,c)=p(a)p(c|a)p(b|c)\tag{9} \end{eqnarray}$

$a,b$ の独立性を調べるため、式 $(5)$ を $c$ で周辺化します。

$\begin{eqnarray} p(a,b)&=&\sum_cp(a|c)p(b|c)p(c)\\ &=&p(a)p(b|a)\tag{10} \end{eqnarray}$

式 $(10)$ の最後の変形ですが、 $p(a,b)$ に確率の乗法定理を適用しているだけで、あまり意味はありません。

式 $(10)$ は一般には $p(a)p(b)$ の形には書けないので、

$\begin{eqnarray} a\mathop{\not\perp\!\!\!\!\!\!\perp}b|\emptyset\tag{11} \end{eqnarray}$

が言えます。

$c$ が観測されたとします。この時、グラフは以下のようになります。

図4: $c$ が観測された時のhead-to-tail
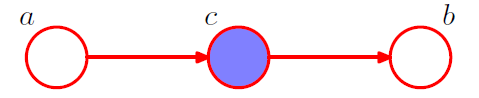
f:id:olj611:20210930021517p:plain:w300

図4の有向グラフより、同時分布を書くと次のようになります。

$\begin{eqnarray} p(a,b|c)&=&\frac{p(a,b,c)}{p(c)}\\ &=&\frac{p(a)p(c|a)p(b|c)}{p(c)}\\ &=&p(a|c)p(b|c)\tag{12} \end{eqnarray}$

式 $(12)$ より、

$\begin{eqnarray} a\mathop{\perp\!\!\!\!\perp}b|c\tag{13} \end{eqnarray}$

が言えます。

これは元々独立ではなかった $a,b$ が、 $c$ が観測されたことにより、独立になったことを意味しています。
head-to-tailとtail-to-tailは同じような現象になりました。

head-to-head

最後に、head-to-headです。
$c$ が2本のリンクの矢印の先(英語でhead)で接続しているので、head-to-headといいます。
$c$ が未観測の時のグラフは以下のようになります。

図5: $c$ が未観測の時のhead-to-head
f:id:olj611:20210930021532p:plain:w250

図5の有向グラフより、同時分布を書くと次のようになります。

$\begin{eqnarray} p(a,b,c)=p(a)p(b)p(c|a,b)\tag{14} \end{eqnarray}$

$a,b$ の独立性を調べるため、式 $(14)$ を $c$ で周辺化します。

$\begin{eqnarray} p(a,b)&=&\sum_cp(a)p(b)p(c|a,b)\\ &=&p(a)p(b)\tag{15} \end{eqnarray}$

よって、先の2例とは異なり、どの変数も観測されていないとき $a$ と $b$ は独立であることが分かります。
この時、

$\begin{eqnarray} a\mathop{\perp\!\!\!\!\perp}b|\emptyset\tag{16} \end{eqnarray}$

がいえます。

$c$ が観測されたとします。この時、グラフは以下のようになります。

図6: $c$ が観測された時のhead-to-head
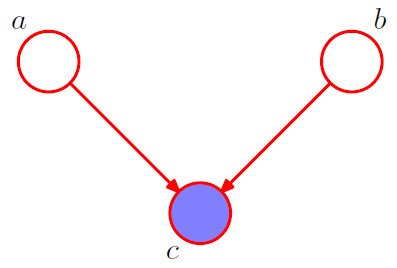
f:id:olj611:20210930021545p:plain:w250

図6の有向グラフより、同時分布を書くと次のようになります。

$\begin{eqnarray} p(a,b|c)&=&\frac{p(a,b,c)}{p(c)}\\ &=&\frac{p(a)p(b)p(c|a,b)}{p(c)}\tag{17} \end{eqnarray}$

式 $(17)$ は一般に積 $p(a|c)p(b|c)$ の形に因数分解できない為、

$\begin{eqnarray} a\mathop{\not\perp\!\!\!\!\!\!\perp}b|c\tag{18} \end{eqnarray}$

です。
これは元々独立であった $a,b$ が、 $c$ が観測されたことにより、独立とはいえなくなった(遮断が解かれた)ことを意味しています。

また、 $c$ に子孫があり、 $c$ は観測されずにその子孫が観測されても、 $a,b$ の遮断が解かれます。(証明についてはPRML演習問題 8.10(基本)参照)

このように、 $c$ や $c$ の子孫が観測されることにより経路が遮断されることを弁明というようです。

有向分離

一般の有向グラフを考えます。
$A,B,C$ をそれぞれ重複しないノード集合とします。
$A,B,C$ を合わせたときにグラフ全体にならなくてもよいです。
この時、有向グラフが $A\mathop{\perp\!\!\!\!\perp}B|C$ を示唆するかは次の $(a),(b)$ で判断できます。
$A$ に属する任意のノードから $B$ に属する任意のノードへの全ての可能な経路のうち、
$(a),(b)$ を満たすノードを含む経路は遮断されているといいます。

$(a)$ ：集合 $C$ に含まれるノードであって、経路に含まれる矢印がそこでhead-to-tailまたはtail-to-tailである
$(b)$ ：経路に含まれる矢印がそのノードでhead-to-headであり、自身あるいはそのすべての子孫のいずれもが集合Cに含まれない。

全ての経路が遮断されていれば、 $A$ は $C$ によって $B$ から有向分離されていると言い、
グラフの全変数上の同時分布は $A\mathop{\perp\!\!\!\!\perp}B|C$ を満たします。

有向分離の例

図7
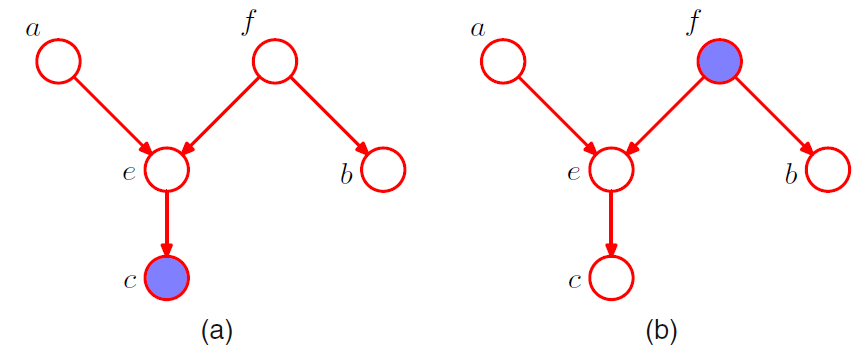
f:id:olj611:20210930030718p:plain:h250

図7を用いて、有向分離の例を示します。
※有向分離の条件 $(a),(b)$ と図7の $(a),(b)$ は関連がありません。

まずは、グラフ $(a)$ における有向分離されない例です。

$a$ から $b$ への経路はノード $f$ によって、遮断されません。
この経路において、ノード $f$ はtail-to-tailでありかつ観測されていない為です。

さらに、この経路はノード $e$ によって、遮断されません。
この経路において、ノード $e$ はhead-to-headですが、その子孫ノード $c$ が観測されている為です。

よって、グラフ $(a)$ において $a\mathop{\perp\!\!\!\!\perp}b|c$ は導けません。

次に、グラフ $(b)$ における有向分離される例です。

$a$ から $b$ への経路はノード $f$ によって、遮断されます。
この経路において、ノード $f$ はtail-to-tailでありかつ観測されている為です。
よって、グラフ $(b)$ において $a\mathop{\perp\!\!\!\!\perp}b|f$ が導けます。

さらに、この経路はノード $e$ によって、遮断されます。
この経路において、ノード $e$ はhead-to-headですが、ノード $e$ 自身とその子孫ノード $c$ が観測されていない為です。

マルコフブランケット

$D$ 個のノードを持つ有向グラフで表現される同時分布 $p({\bf x}_1,\ldots,{\bf x}_D)$ と、変数 ${\bf x}_i$ に対応するノード上の、
他の全ての変数 ${\bf x}_{j\not=i}$ で条件づけられた条件付き分布を考えます。
条件付き分布は次のように書けます。

$\begin{eqnarray} p({\bf x}_i|{\bf x}_{j\not=i})&=&\frac{p({\bf x}_1,\ldots,{\bf x}_D)}{p({\bf x}_1,\ldots,{\bf x}_{i-1},{\bf x}_{i+1},\ldots,{\bf x}_D)}\\ &=&\dfrac{p({\bf x}_1,\ldots,{\bf x}_D)}{\displaystyle\int p({\bf x}_1,\ldots,{\bf x}_D){\rm d}{\bf x}_i}\\ &=&\dfrac{\displaystyle\prod_kp({\bf x}_k|pa_k)}{\displaystyle\int \displaystyle\prod_kp({\bf x}_k|pa_k){\rm d}{\bf x}_i}\tag{19} \end{eqnarray}$

式 $(19)$ において、因数 $p({\bf x}_k|pa_k)$ は ${\bf x}_k\not={\bf x}_i$ かつ ${\bf x}_i\not\in pa_k$ のとき、分子と分母に存在するので約分されます。
( ${\bf x}_i$ に無関係な因数は式 $(19)$ から消えるってことです。)
ですので、残る因数は $p({\bf x}_i|pa_i)$ と $p({\bf x}_k|pa_k)\ ({\bf x}_i\in pa_k)$ です。
$p({\bf x}_i|pa_i)$ はノード ${\bf x}_i$ の親に依存し、 $p({\bf x}_k|pa_k)$ はノード ${\bf x}_i$ の子とその共同親に依存します。
( $p({\bf x}_k|pa_k)$ の ${\bf x}_k$ は親に ${\bf x}_i$ を含むので、 ${\bf x}_i$ の子です。)
共同親とは、ノード ${\bf x}_k$ の親のうちノード ${\bf x}_i$ 以外のものを指します。

以下の図8は、マルコフブランケットと呼ばれる、親、子及び共同親からなるノード集合です。

図8
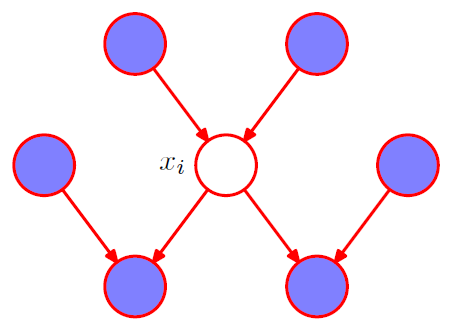
f:id:olj611:20210930030558p:plain:w300

ノード ${\bf x}_i$ のマルコフブランケットは、 ${\bf x}_i$ を残りのグラフからから孤立させるためのノードの最小集合と考えることができます。
マルコフブランケットはノード ${\bf x}_i$ の親と子だけからなるのではないので注意が必要です。
なぜなら弁明現象ににより、子ノードの観測によって共同親への経路の遮断が解かれるためです。

したがって、 $p({\bf x}_i|{\bf x}_{j\not=i})$ の値を得るためには全ての共同親ノードも観測しなくてはなりません。

マルコフブランケット以外の残りの変数に対して、独立であることを有向分離基準を用いた証明は、
PRML演習問題 8.9(基本) wwwを参照してください。

最後に

有向分離については、おすすめのブログがありまして、
有向分離を使いこなす！～有向分離の導入と教師有り学習～にシステマチックな手法で有向分離を判断する記事が掲載されています。

偉人の名言

f:id:olj611:20210930030523p:plain:w300
努力によって得られる習慣だけが善である。
カント

参考文献

パターン認識と機械学習下巻 p84-p96

動画

なし